Update September 10: We have made a small extension to the due date. Please see the timeline below for details.
Update August 26: Please see Questions and Answers below for answers to questions posed by participants.
Update August 19: This website has been updated: 1. to clarify how comparisons will be made across implementations of different algorithms (see "Algorithm Choice and Clustering Accuracy"); 2. to provide details of the prize amounts (see "Prizes").
k-Means clustering is an unsupervised method for clustering multidimensional data points, aiming to partition the points into \(k\) subgroups (clusters) that are similar. This is used in a variety of applications such as data mining, image segmentation, medical imaging, and bioinformatics. The 2016 MEMOCODE Design Contest problem is to implement a hardware or software system to efficiently compute k-means clustering on a large dataset.
Below you will find descriptions of: the problem, example datasets, and a functional reference implementation. For instructions to download the code and datasets, please sign up by e-mailing Peter Milder at peter.milder@stonybrook.edu with your team information (names of participants, affiliations, and a team name).
Participants will have approximately one month to develop systems to solve this problem. A $500 prize will be awarded to each of two winning teams: the team with the best absolute performance and the team with the best cost-adjusted performance. (See details below.) Each team delivering a complete and working solution will be invited to prepare a 2-page abstract to be published in the proceedings and to present it during a dedicated poster session at the conference. The winning teams will be invited to contribute a 4-page short paper for presentation in the conference program.
The contest is open to industry and academic participation. A team may include both industry and academic members. There is no limit on the number of members of a team, or the number of teams per institution. However, each person may participate in only one team.
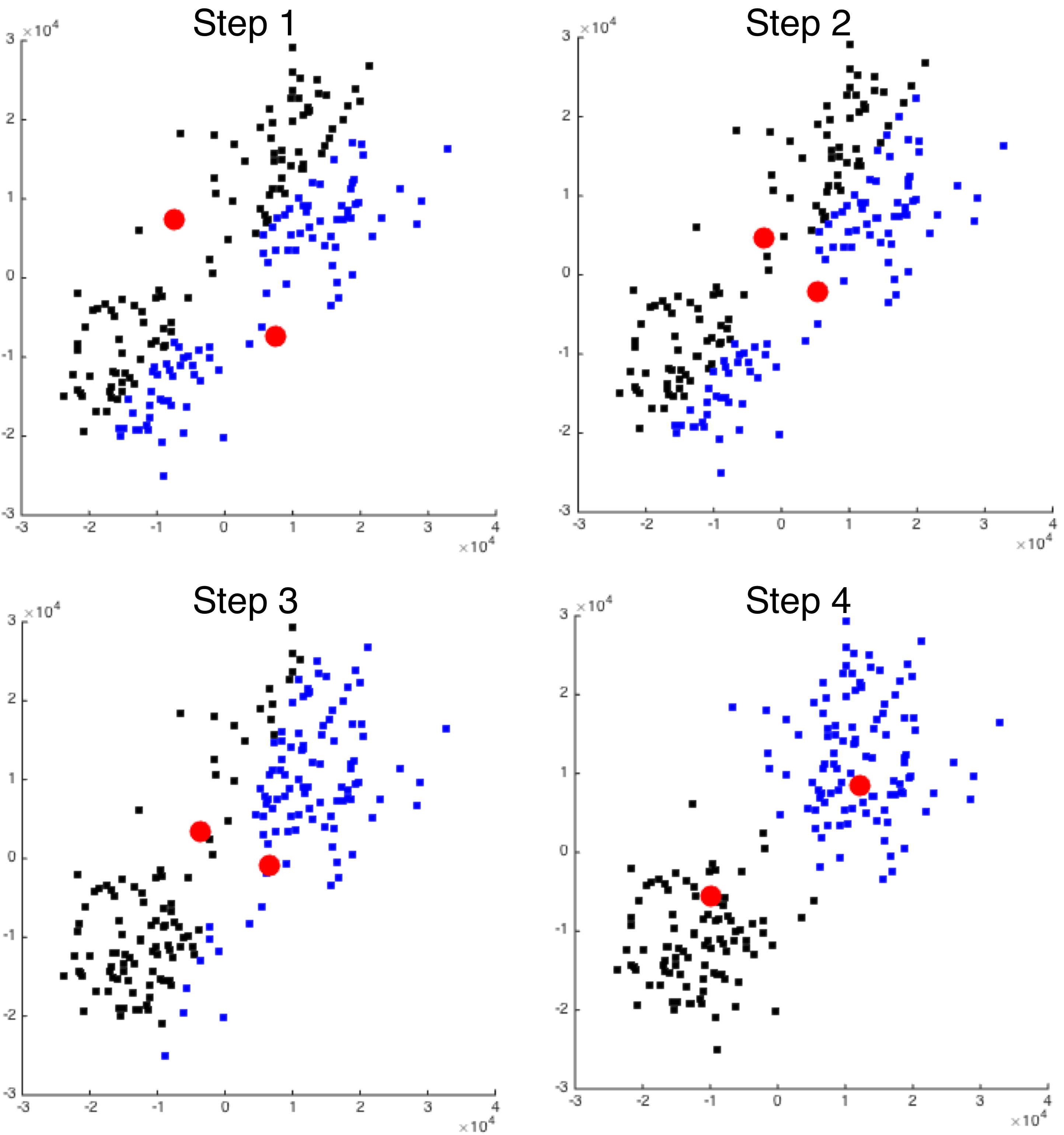
The image below illustrates a simple example performing k-means clustering on two-dimensional data. The black and blue squares represent the data we want to cluster, and the large red circles show the centers of our \(k=2\) clusters. Initially (Step 1), the cluster centers are randomly-generated; the squares are colored black or blue to indicate which of the two clusters each point belongs to. The black-colored points are those closest to the top-left center, and the blue-colored points are those closest to the bottom-right center.

We can easily see in Step 1 that our randomly-chosen centers are not well-placed with respect to the data. The algorithm proceeds by re-calculating the location of each center as the mean value of all the points within its cluster. That is, the top-left red circle's location gets moved to the mean of the locations of all the black squares, and the bottom-right red circle's location gets moved to the mean of the locations of all the blue squares.
The algorithm then proceeds iteratively. In the next iteration (Step 2), the same sequence of operations are performed. First, each of the data points is compared with the locations of the centers, and is assigned to the closest cluster. Then, the centers' locations are again updated by averaging the locations of each element in the cluster.
As each iteration proceeds, the centers will move to better cluster the data. We can see that by Step 3 the blue and black dots are becoming better separated; by Step 4 they are fully separated. The iterative algorithm will repeat until it converges or a fixed number of iterations are reached.
Problem Definition:
Let \(D\) represent a set of observations consisting of \(n\) elements \(d_0, \dots, d_{n-1}\), each representing a point in \(m\)-dimensional space. Our goal is to partition these \(n\) points into \(k\) clusters \(S_0,\dots,S_{k-1}\) that minimizes the distances between each element in \(D\) and the center of its nearest cluster.
That is, the goal is to partition \(D\) into \(k\) clusters \(S_i\) that minimizes
$$ \sum_{i=0}^{k-1}\sum_{d\in S_i} \lVert d-\mu_i\rVert^2,$$
where \(\mu_i\) is the center (average) of all points assigned to cluster \(S_i\), and distance is quantified using squared-Euclidean distance:
$$\lVert a-b \rVert^2 = \sum_{i=1}^{m} (a_i-b_i)^2,$$
where \(a_i\) and \(b_i\) represent the \(i\)-th dimension of the \(m\)-dimensional \(a\) and \(b\) vectors. Note that we use squared Euclidean distance to avoid an unnecessary square-root operation.
Heuristic Algorithm
The most common method for performing this clustering is an iterative refinement method called Lloyd's algorithm [1]. Given a set of \(k\) initial cluster centers \(\mu_0,\dots,\mu_{k-1}\), each iteration performs the following two steps:
These two steps repeat until the algorithm converges or a fixed number of iterations are reached. For the purposes of this contest, we will employ a fixed-number of iterations.
A naive solution (such as in the functional reference handout) will perform the assignment step by comparing all \(d_j\) to all \(\mu_i\); other algorithms that reduce this cost have been explored in hardware and software.
Your system will take as input:
In each iteration your system must: (1) find, for each of the \(n\) points, which of the \(k\) clusters is closest to it based on the squared Euclidean distance metric, and (2) calculate the new center of each cluster as the average of locations for each point assigned to it.
Your system will produce as output:
The timed portion of your solution must start with all input data in main system memory, and it must conclude with all output data in main memory.
This section added August 19 to clarify how we will evaluate implementations that use different algorithms.
Different algorithms for performing this clustering can result in differing numbers of iterations (i.e., a given algorithm may reach the same quality of results in fewer iterations), or they may converge on a different local minima. For this reason, we will allow any algorithm to be used so long as it reaches a solution "as good" as the naive reference algorithm, as measured by the sum of the squared Euclidean distances of each the point from its nearest center. That is: $$ \text{total distance} = \sum_{i=0}^{k-1}\sum_{d\in S_i} \lVert d-\mu_i\rVert^2, $$ where \(\mu_i\) is the center (average) of all points assigned to cluster \(S_i\), and: $$\lVert a-b \rVert^2 = \sum_{i=1}^{m} (a_i-b_i)^2,$$
where \(a_i\) and \(b_i\) represent the \(i\)-th dimension of the \(m\)-dimensional \(a\) and \(b\) vectors.
With the "large" dataset, we have included the target distance that must be reached. (Note that if you use Lloyd's algorithm or an equivalent, this will be reached in the specified number of iterations.) Version 1.1 of the handout code also contains a post-processing function that you can use to calculate the final distance of your solution.
Please note: if you have already downloaded the initial version of the reference code and data, we have adjusted the number of iterations for the large dataset, but not the data itself.
Elements in \(D\) are given as signed integers. The range of the input values is limited such that every input element can be represented as a 16-bit signed value.
The final output values are: (1) the labels of each input element in \(D\) (thus, unsigned integers between \(0\) and \(k-1\)), and (2) the set of \(k\) cluster centers in \(m\)-dimensional space (where each is a signed integer value).
Designers may choose to optimize the datatype as appropriate. There is no constraint on the order that the results are reported; for convenience the reference code sorts them before storing to a file. (The time for this operation is not included in our timing measurements, see below.)
We are providing a naive software implementation to serve as a functional reference for the contestants' optimized implementations. The reference implementation reads parameters that specify data dimensions, and the input files for the dataset \(D\) and initial cluster locations. It computes the given number of iterations, and stores the result.
Based on the problem definition, the order of the output values does not matter. For convenience, the functional reference performs post-processing to sort them based on the location; this will allow an easy use of diff to determine if two output files are equivalent. This sorting does not need to be in your implementation (and its runtime is be ignored).
Lastly, a Makefile is provided; typing “make runsmall” at the command line will compile the software, run it on a small example dataset, and verify the correctness of the results. For more information on the reference software and its inputs and outputs, please see readme.txt included with the software.
Three datasets are provided to aid in validation and development. Each set contains a \(m\)-dimensional input dataset \(D\) and the initial values of the center locations. Each set is accompanied by a reference solution that provides the sorted center locations and accompanying labels for each input value.
The three datasets provided are named small, medium, and large. More information about the dataset input and output file names and instructions are included in readme.txt. Typing “make runsmall” at the command line will compile the reference design, run it on the small example dataset, and verify correctness of the results.
Contestants have approximately one month to implement the system using their choice of platforms such as FPGAs, CPUs, GPGPUs, etc. The system must be validated using the supplied reference inputs and outputs discussed above.
Contest winners will be selected based on the performance of their systems. Performance will be measured using a dataset that has the same size \(n,k,m\) as the "large" dataset. The time taken to initialize data and read out the results is excluded from the run time measurement. (See also the comments in reference software's main function.)
As in previous design contests, winners will be chosen in two categories. First, the “pure-performance” award will be based only on the fastest runtime. Second, the “cost-adjusted-performance” award will be chosen by multiplying runtime by cost of the system. For example, a $100 system with runtime of 60 seconds is equivalent to $200 system with runtime of 30 seconds. The cost of the system is based on the lowest listed prices (academic or retail). If no price is available (e.g., using an experimental platform), judges will estimate the system cost. Contestants are requested to submit cost estimates of their systems to aid in judging.
For instructions to download the code and datasets, please sign up by e-mailing Peter Milder at peter.milder@stonybrook.edu with your team information.
Before 11:59PM US Eastern Time on September 13, 2016, submit your design solution in a tar or zip file to peter.milder@stonybrook.edu
After your submission you will receive a confirmation email within 24 hours. If you do not receive this information email after 24 hours, please contact peter.milder@stonybrook.edu
Your submission should contain the following items in a single zip or tar file:
Documentation in the form of PowerPoint slides is perfectly acceptable. The quality and conciseness of the documentation will help in judging. The judges will make a best effort to treat the design source files as confidential. The information in other items is considered public.
If you have any questions, please contact Peter Milder.
Contest starts: August 15, 2016
Submissions due: September 13, 2016 September 17, 2016
Winners announced: September 15, 2016 September 19, 2016
Papers/abstracts due: October 7, 2016 October 11, 2016
Is it permissible to use a different method for computing the clusters' centers?
Yes, your algorithm can use any method you like for determining the center of the clusters, however in the end the system must meet the overall distance constraint as measured using squared Euclidean distance as described above.
What should we do if two or more clusters collapse (where one or more centers has no points in its cluster)?
We have checked to make sure that this will not happen for our dataset if you are using the reference algorithm (Lloyd's) or one that performs equivalently. If you are using other methods, you may choose how to handle this situation. However keep in mind that the final result must meet the overall distance constraint.
[1] Stuart P. Lloyd. "Least Squares Quantization in PCM." IEEE Transactions on Information Theory, Vol. IT-28, No. 2, March 1982.
Peter Milder, peter.milder@stonybrook.edu
This page uses MathJax for displaying mathematical formulas. If your browser has Javascript disabled, formulas will not display correctly.
Previously: 2015 MEMOCODE Design Contest. 2014 MEMOCODE Design Contest.